How to Determine Coordination Environments Algorithmically.
How can we algorithmically determine the coordination environment of any atomic site in a crystal structure, given only the atomic position vectors? Three common critertia for such determinations are presented below.
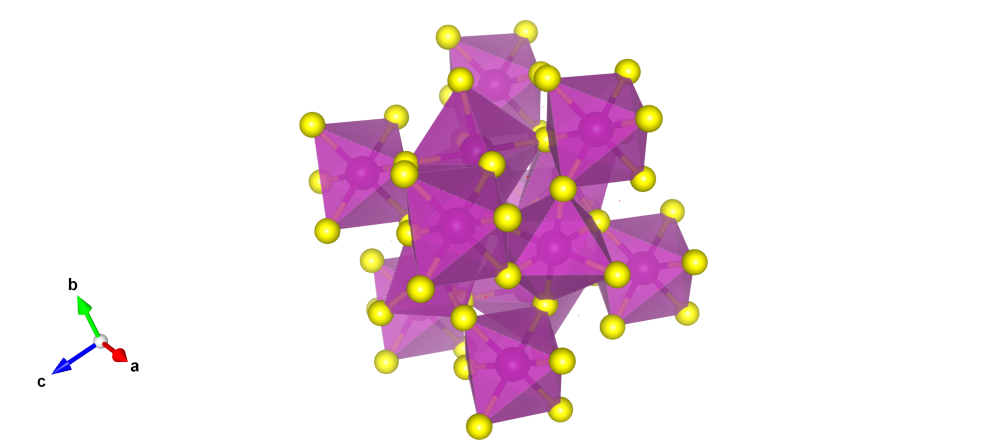
In chemistry or solid state physics, it often is neccessary to determine the most relevant set of neighbors for each site of some periodic structure. This local bonding environment often resembles some perfect polyhedral structure (e.g. so-called 'motifs' in minerals, as in Pauling's Rul es). The coordination environment of an atomic site is exactly this local environment formed from these most relevant neighbors. As an example, consider the octahedral structure formed by six sulfur atoms around each Manganese atom in Cubic MnS, as shown below:
For modern applications, the determination of a given site's coordination environment is often done computationally, that is, algorithmically; however, there is no real 'right' way to determine a relevant coordination environment, just better and worse ways for different intended applications. With that in mind, several common criteria are presented below; and then several real determination schemes are examined. All below methods are given as examples in pymatgen.
Common Criteria
Three basic geometric concepts are very commonly used in most real applications: interatomic distance, Voronoi tesselation, and solid angle. Interatomic distance is self-explanatory and of obvious importance. Solid angles are those spanned from each atomic site by a neighbor's adjoining face in a Voronoi tesselation, where a Voronoi tesselation is a partitioning of space between atomic sites, in which each partition marks the space where the corresponding atomic site is the closest.
All three of these concepts are covered below (as necessary). To illustrate each concept's relevance, an example neighbor-finding scheme based on it is then presented, alongside it's implementation in pymatgen where possible.
Interatomic Distance
Interatomic distance is simply the distance between the centers of atomic sites in a crystal structure.

A more informed approach might consider the usual bonding distance for atomic pairs, and use that as a relative scale for determination. One could alternatively limit considered pairs of a coordination enviroment to those within some tolerance of the sum of the usual ionic bonding radii of the two atoms of the pair. But these methods obviously require the additional information of usual bond lengths and ionic bonding radii.
Example: Scaled Nearest Neighbor Distance
A common, lightweight scheme for neighbor determination is a scaled nearest neighbor distance. That is, we consider neighbors to be those with interatomic distance \(d\) below the threshold: \[ d<(1+\delta)d_{min} \] where \(\delta\) is the tolerance factor (~0.1+), and \(d_{min}\) is the interatomic distance of the center site's nearest neighbor (~2-4 Angstrom for most crystals).
This strategy can be implemented in pymatgen to get the nearest neighbors of a pymatgen.Structure object's sites as mindNN. Using this on the usual example of Manganese Sulfide with a default tolerance of 0.1, we get the seemingly appropriate neighbor set describing the expected octahedral structure.
Voronoi Tesselation
A Voronoi diagram is a partition of the space containg some set of points, such that each
section of the partition corresponds to that part of space which is closest to it's corresponding 'center' site.
As a fun fact, the Voronoi partition of any set of points may be visualized as being formed by cirlces centered at each point of interest expanding at a
constant, equal rate until colliding, where they stop to form the boundaries:

A tesselation is similar to a tiling, in that it's a periodic structure that completely fills a space with no overlaps or voids. In the case of a Voronoi tesselation then, the 'tiles' are centered about a periodic set of center sites, and are exactly the cells of it's corresponding Voronoi diagram.
The Voronoi tesselation of a crystal (based around it's atomic sites) is necessarily periodic as it's underlying structure is. The cells of these tesselations are, in fact, the Wigner-Seitz cells well known
to crystalographers and solid state physicists. Such tesselations are particularly handy since they afford us some way to assign each point in space to some
site definitively; and more importantly here, they allow us another method by which we may look for neighboring sites.

Example: Face-sharing Neighbors
The simplest scheme for neighbor determination utilizing the Voronoi tesselation is one that considers all those sites sharing a face between their corresponding Voronoi cells to be neigbbors.
This method is available in pymatgen as the VoronoiNN class. Using this on the usual example of Manganese Sulfide with the default settings (that is, tolerance = 0) gives a larger set of neighbors for each site than would be expected for our exemplary octahedral structure.
Solid Angle
With the Voronoi tesselation in hand, we may further define another common concept, that of the solid angle spanned by neighboring sites. The solid angle here is that swept out
by the shared face of the adjoining Voronoi cells, as below.

For example, in the case of cubic Manganese Sulfide, two Manganese atoms may share a Voronoi face, but this shared face will sweep out a much smaller solid angle than that formed by it's Sulfur atom adjoining faces. An example of a scheme implenting such a solid-angle criteria in addtion to a Voronoi tesselation is given below.
Example: Scaled Maximum Solid Angle
Much like the scaled minimum interatomic distance scheme, we now may scale the largest solid angle swept by any of a site's adjoining Voroni cell faces and and use it as a cutoff for potential neighbors. So, we may accept neighbors only if they share a Voronoi face that sweeps out a solid angle \(\Omega\) that abides by the cutoff: \[ \Omega > \delta\Omega_{max} \] where \(\delta\) is a tolerance, and \(\Omega_{max}\) is the largest solid angle of the center site's cell.
This is available in pymatgen as the VoronoiNN class again, now by setting the tolerance of the form above (by passing the key word argument 'tol'). Using this on the usual example of Manganese Sulfide with a tolerance of 0.8 gives the neighbor set expected for the octahedral structure around Manganese.
What About Atomic Information?
Another key bit of information we may consider is the usual bonding behaviour of certain atom pairs. For example, in Sodium Chloride, one could certainly make the argument that we should simply say it's coordination environment is formed by it's closest set of oppositely charged atoms. That is, we also may consider the usual bonding behaviours of potential pairs implicit in a coordination environment in it's determination.

This may also be implemented algorithmically, but it requires additional information beyond just the geometrical structure of the crystal. This additional information is the oxidation state of each site in the crystal strucutre. If not known already, the oxidation state of a given compound may often be guessed by just considering the usual oxidation states of the atoms in other compounds (see oxi_state_guesses and add_charges_from_oxi_state_guesses for a pymatgen implementation. ).
CrystalNN, as implemented in pymatgen, can utilize the oxidation states to determine coordination environments accordingly. This is in addition to a unique plane-orientation minimization strategy.
Conclusion
Since there is no perfect method for coordination enviroment determination, it's best to have a general understanding of several common concepts and techniques so one may choose that best suited for the application at hand. Some computational tasks may prefer more economical compute times, while other more application-driven techniques may seek to incorporate as much physical insight as possible. As such, the basic concepts such as solid angle and Voronoi tesselation are given above.
